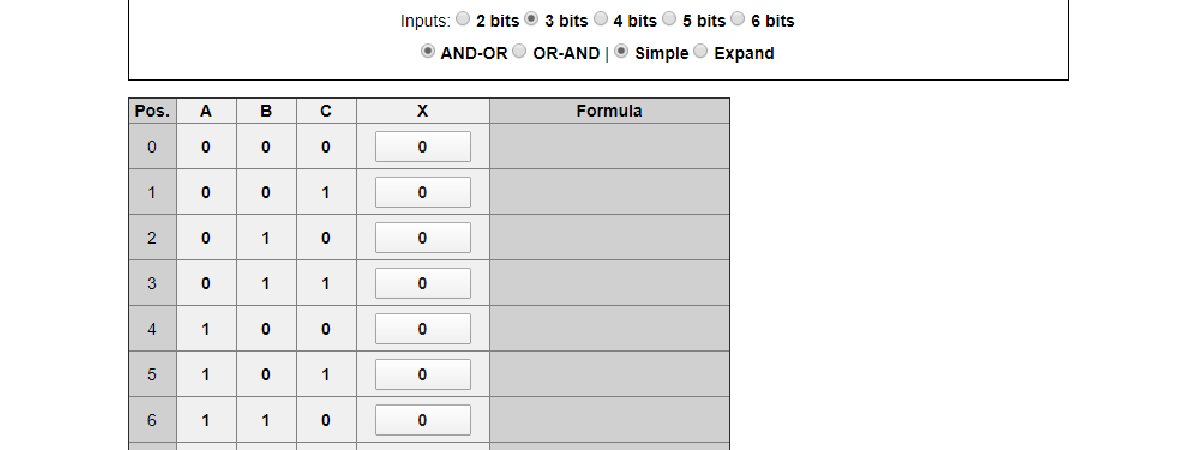
Tabella della verità interattiva
Le Tabelle della verità vengono usate in elettronica digitale per descrivere il comportamento di circuiti con N ingressi (A, B, C) ed un uscita (X).
Sugli ingressi vengono riportate tutte le possibili combinazioni, mentre sull'uscita viene impostato lo stato che il circuiti deve assumere.
Fatto questo è possibile ricavare la formula che rappresenta il circuito prendendo in considerazione le uscite a 1 (AND-OR) o a 0 (OR-AND).
Guardando la tabella di verità si vede che bits a 1 in numero pari sono nella posizione 3, 5 e 6. Quindi usando AND-OR la formula risultante è X = (!A*B*C)+(A*!B*C)+(A*B*!C) che diventa il seguente circuito logico realizzato con porte AND e OR:
Si può fare un altra semplificazione, in quanto (!A + A) è un OR tra un valore e la sua negazione, quindi darà sempre come risultato 1.
La formula a questo punto diventa X = (!B * C) * 1 ovvero X = !B * C.
Sugli ingressi vengono riportate tutte le possibili combinazioni, mentre sull'uscita viene impostato lo stato che il circuiti deve assumere.
Fatto questo è possibile ricavare la formula che rappresenta il circuito prendendo in considerazione le uscite a 1 (AND-OR) o a 0 (OR-AND).
Inputs:
Outputs:
Clicca sull'uscita X per cambiare lo stato e vedere la formula che descrive il circuito.
L'opzione Simple visualizza le formule secondo la notazione convenzionale mentre Expand visualizza le formule in una forma più adatta ad un eventuale copia e incolla.
L'opzione Simple visualizza le formule secondo la notazione convenzionale mentre Expand visualizza le formule in una forma più adatta ad un eventuale copia e incolla.
Il numero di combinazioni degli ingressi è dato da 2^N (2 elevato al numero di ingressi, dove il 2 rappresenta la base, ovvero 2 simboli disponibili, 0 e 1)
Va tenuto presente che:- il simbolo * (asterisco o moltiplicazione logica) indica la funzione AND (può anche essere omesso)
- il simbolo + (più o somma logica) indica la funzione OR
- il simbolo ! (not logico) o la linea sopra la lettere indica la funzione NOT (negazione)
- il simbolo 1 indica lo stato vero
- il simbolo 0 indica lo stato falso
Esempio 1
Fare un circuito di controllo parità che, dati 3 ingressi (A, B e C) dia un uscita (X) a 1 quando gli ingressi a 1 sono in numero pari.Guardando la tabella di verità si vede che bits a 1 in numero pari sono nella posizione 3, 5 e 6. Quindi usando AND-OR la formula risultante è X = (!A*B*C)+(A*!B*C)+(A*B*!C) che diventa il seguente circuito logico realizzato con porte AND e OR:
Circiti logici X = (!A*B*C)+(A*!B*C)+(A*B*!C) - Sgart.it
X
Attendi il caricamento ...
Puoi interagire le simulazioni dei circuiti logici cliccando sugli ingressi A, B e C
Esempio 2
La funzione di XNOR (o EX-NOR) con due ingressi deve dare 1 nella posizione 0 (A=0, B=0) e nella posizione 3 (A=1, B=1), ed è descritta dalla formula X = (!A*!B)+(A*B) il cui circuito logico è:Circiti logici X = (!A*!B)+(A*B) - Sgart.it
X
Attendi il caricamento ...
Esempio 3
Le formule possono essere semplificate usando le normali regole matematiche. Ad esempio la formula X = (!A*!B*C)+(A*!B*C) può essere scritta come X = (!B * C) * (!A + A) .Si può fare un altra semplificazione, in quanto (!A + A) è un OR tra un valore e la sua negazione, quindi darà sempre come risultato 1.
La formula a questo punto diventa X = (!B * C) * 1 ovvero X = !B * C.
Circiti logici X = !B * C - Sgart.it
X
Attendi il caricamento ...