Circuito sommatore digitale
In elettronica digitale il sommatore è uno dei circuiti di base ed è implementato in tutte le ALU delle CPU.
Per capire come funziona un sommatore digitale bisogna partire dal sommatore di 2 bit.
Questo circuito è composto di base da una porta XOR, che serve per realizzare la somma dei 2 bit, e da una porta AND per calcolare il riporto quando la somma non può essere contenuta in 1 bit.
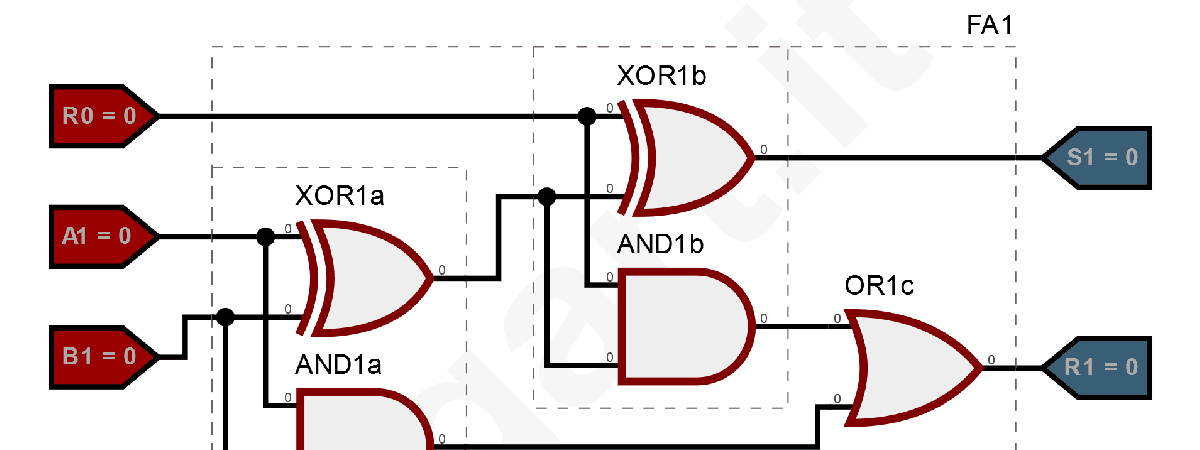
In questo caso bisogna avere un circuito Full Adder (FA) composto da due HA e una porta OR sui riporti:
Nell'esempio seguente ne riporto uno a 4 bit:
Per capire come funziona un sommatore digitale bisogna partire dal sommatore di 2 bit.
Questo circuito è composto di base da una porta XOR, che serve per realizzare la somma dei 2 bit, e da una porta AND per calcolare il riporto quando la somma non può essere contenuta in 1 bit.
Per la tabella della verità vedi il simulatore di porte logiche.
Questo circuito è detto Half Adder (HA) o semi sommatore digitale:Circiti logici Sommatore - Sgart.it
X
Attendi il caricamento ...
A0 e B0 rappresentano i due bit da sommare, S0 è il risultato della somma e R0 è il riporto (carry).
Cliccando sulgi ingressi A o B puoi interagire con la simulazione.
Cliccando sulgi ingressi A o B puoi interagire con la simulazione.
Su ogni ingresso e uscita delle singole porte logiche è riportato un numero 1 o 0 che rappresenta lo stato di ingresso o uscita attuale.
Quando si hanno più di due bit, è necessario modificare il circuito HA per tenere conto del riporto della somma dei bit precedenti.In questo caso bisogna avere un circuito Full Adder (FA) composto da due HA e una porta OR sui riporti:
Circiti logici Sommatore full - Sgart.it
X
Attendi il caricamento ...
A1 e B1 rappresentano i due bit da sommare, R0 e il riporto della somma dei bit precedenti, S1 è il risultato della somma e R1 è il riporto attuale.
Combinando assieme Half Adder e Full Adder è possibile fare un sommatore a N bit.Nell'esempio seguente ne riporto uno a 4 bit:
Circiti logici Sommatore 4bit - Sgart.it
X
Attendi il caricamento ...
In questo caso A0,A1,A2 e A3 rappresentano i bit del primo numero, mentre, B0,B1,B2 e B3 sono i bit del secondo numero. Il risultato della somma, in bit, è mostrato da S0,S1,S2,S3 e R3.
Da notare come la somme dei bit 0 sia sufficiente un HA in quanto non abbiamo un riporto da considerare, poi tutti gli altri bit richiedono un FA. Ad ogni FA viene portato in ingresso il riporto della somma dei bit precedenti.
Sopra agli ingressi e alle uscite, su ogni bit, ho riportato un numero che rappresenta il peso dello specifico bit ovvero:- bit 0 = base 2^0 = 1
- bit 1 = base 2^1 = 2
- bit 2 = base 2^2 = 4
- bit 3 = base 2^3 = 8
- bit 4 = base 2^4 = 16