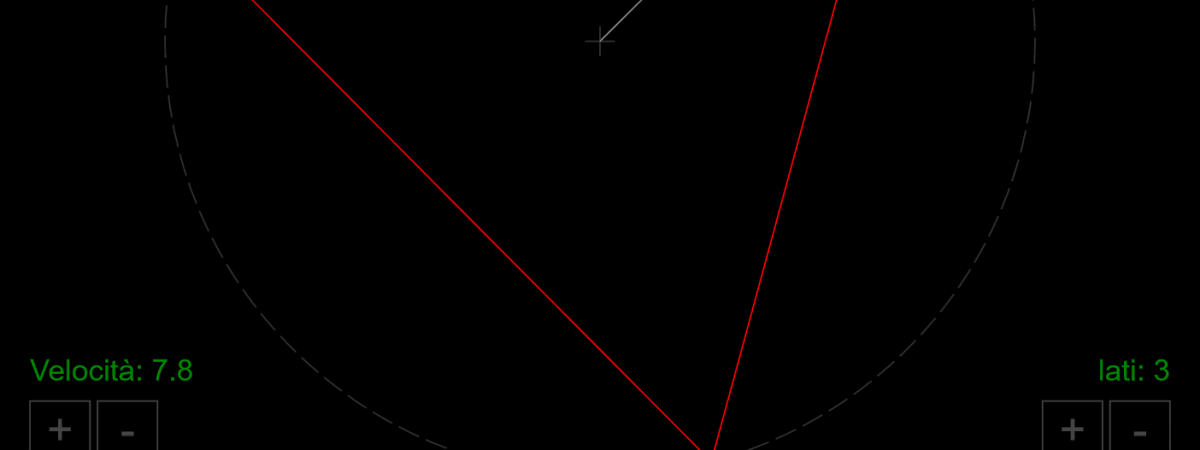
Animazione poligono in JavaScript
Quella riportata qui è la variante in JavaScript dell'animazione creata in MicroPhyton per Raspberry PI Pico.
Fondamentalmente si tratta di realizzare una funzione loop che esegue i calcoli della nuova posizione, in funzione del tempo passato, pulisce e ridisegna gli elementi, ed infine richiama se stessa tramite la funzione di sistema requestAnimationFrame
In particolare le funzioni seno e coseno.
Queste due funzioni, dato l'angolo, ritornano: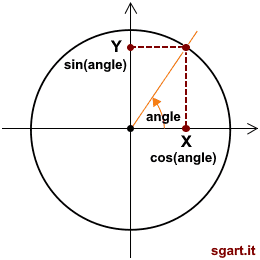
seno e coseno
Per ricavare gli altri vertici dobbiamo introdurre altre variabili.
Oltre all'angolo (segmentAngleInc) ricavato in base al numero dei lati compresi in un angolo giro, serve anche l'attuale angolo di rotazione ed un ciclo per ricavare tutti i vertici
Va però introdotto un nuovo concetto, ovvero la velocità di rotazione (animationSpeedAngle )
Polygon - Sgart.it
X
Attendi il caricamento ...
E' possibile interagire con l'animazione cliccando sui pulsanti + e -.
Gestione animazione
Il concetto su cui si basa l'animazione è descritto qui Creare un animazione in Javascript.Fondamentalmente si tratta di realizzare una funzione loop che esegue i calcoli della nuova posizione, in funzione del tempo passato, pulisce e ridisegna gli elementi, ed infine richiama se stessa tramite la funzione di sistema requestAnimationFrame
JavaScript
/* gestione ciclo di animazione */
let lastTime = new Date();
function loop() {
//calcolo il tempo passato tra un render e l'altro
const current = new Date();
const elapsed = current - lastTime; //circa 16 msec
updatePosition(elapsed);
render();
lastTime = current;
requestAnimationFrame(loop);
}
Tipicamente la funzione requestAnimationFrame viene richiamata ogni 16 millisecondi.
Trigonometria
Trattandosi di una animazione di un solido in rotazione, per calcolare la posizione dei vertici bisogna fare uso di un po' di trigonometria di base.In particolare le funzioni seno e coseno.
Queste due funzioni, dato l'angolo, ritornano:
- seno la proiezione del raggio di lunghezza 1 sull'asse delle Y
- coseno la proiezione del raggio di lunghezza 1 sull'asse delle X

Render e calcoli
Dato un raggio di lunghezza radius, che corrisponde al cerchio in cui sarà inscritto il poligono, un angolo di rotazione angle espresso in radianti e le coordinate del centro del cerchio cx e cy, si possono ricavare le coordinate x e yJavaScript
// angolo giro
var PI_360 = Math.PI * 2;
var segment = 3; // triangolo
var angle= PI_360 / segment;
var radius=15;
var x = cx + Math.cos(angle) * radius;
var y = cy + Math.sin(angle) * radius;
Per ricavare gli altri vertici dobbiamo introdurre altre variabili.
Oltre all'angolo (segmentAngleInc) ricavato in base al numero dei lati compresi in un angolo giro, serve anche l'attuale angolo di rotazione ed un ciclo per ricavare tutti i vertici
JavaScript
var PI_360 = Math.PI * 2;
var segment = 3; // triangolo
var segmentAngleInc = PI_360 / segment;
var angleOffset = 0; // posizione iniziale dell'animazione
function render() {
var cx = canvas.width / 2;
var cy = canvas.height / 2;
var radius = cy - 10;
var segmentAngleInc = PI_360 / segment;
var angle = angleOffset;
// disegno i segmenti del poligono
for (let i = 0; i < segment; i++) {
var x = cx + Math.cos(angle) * radius;
var y = cy + Math.sin(angle) * radius;
/* todo: gestire disegno dei segmenti */
angle += segmentAngleInc;
}
}
Animazione
Trattandosi di un animazione semplice, la funzione updatePosition dovrà solo incrementare l'angolo di rotazione in funzione del tempo passato.Va però introdotto un nuovo concetto, ovvero la velocità di rotazione (animationSpeedAngle )
JavaScript
var animationSpeedAngle = (Math.PI / 180) * 45; // rotazione in gradi che dovrà compiere il solido in un secondo
function updatePosition(elapsed) {
if (elapsed === 0) {
elapsed = 16;
}
angleOffset += animationSpeedAngle * elapsed / 1000;
if (angleOffset >= PI_360) {
// se supero i 360 gradi riparto da 0
angleOffset = angleOffset % PI_360;
}
}
Codice completo
Il codice completo dell'animazione è questo:JavaScript
/**
* sgart-polygon.js
* animazione di un poligono in rotazione
* https://www.sgart.it/IT/informatica/animazione-poligono-in-javascript/post
*/
(function (idTemplate) {
'use strict';
const CANVAS_WIDTH = 640;
const CANVAS_HEIGHT = 480;
// numero di lati del poligono
var segment = 3;
var SEGMENT_MIN = 3;
var SEGMENT_MAX = 40;
var SEGMENT_INC = 1;
// velocità di rotazione gradi al secondo
var animationSpeedAngle = (Math.PI / 180) * 45;
var SPEED_MIN = (Math.PI / 180) * 1;
var SPEED_MAX = (Math.PI / 180) * 360 * 2;
var SPEED_INC = SPEED_MIN * 1;
var SPEED_INC_10 = SPEED_MIN * 15;
// valore corrente dell'angolo di rotazione
var angleOffset = -Math.PI / 2; // posizione iniziale dell'animazione
var mouse = {
x: 0,
y: 0,
down: false
};
var zoom = 1;
// buttons
var btnSegmentPlus;
var btnSegmentMinus;
var btnSpeedPlus;
var btnSpeedMinus;
// init canvas
var wrapper;
var canvas;
var ctx;
// fattore di conversione radianti in gradi
var RAD_DEG = 180 / Math.PI;
// angolo giro
var PI_360 = Math.PI * 2;
function updatePosition(elapsed) {
if (elapsed === 0) {
elapsed = 16;
}
angleOffset += animationSpeedAngle * elapsed / 1000;
if (angleOffset >= PI_360) {
// se supero i 360 gradi riparto da 0
angleOffset = angleOffset % PI_360;
}
}
function render() {
var cx = canvas.width / 2;
var cy = canvas.height / 2;
var radius = cy - 10;
var segmentAngleInc = PI_360 / segment;
var angle = angleOffset;
// riempio lo sfonfo
ctx.fillStyle = "#000";
ctx.rect(0, 0, canvas.width, canvas.height);
ctx.fill();
// disegno il cerchio
ctx.beginPath();
ctx.strokeStyle = "#333";
ctx.setLineDash([15, 5]);
ctx.arc(cx, cy, radius, 0, PI_360, false);
ctx.stroke();
// disegno la croce al centro
ctx.setLineDash([]);
var sl = 10;
ctx.beginPath();
ctx.moveTo(cx - sl, cy);
ctx.lineTo(cx + sl, cy)
ctx.moveTo(cx, cy - sl);
ctx.lineTo(cx, cy + sl)
ctx.stroke();
// disegno i segmenti del poligono
for (let i = 0; i < segment; i++) {
var x = cx + Math.cos(angle) * radius;
var y = cy + Math.sin(angle) * radius;
if (i == 0) {
ctx.beginPath();
ctx.strokeStyle = "#888";
ctx.moveTo(cx, cy);
ctx.lineTo(x, y);
ctx.stroke();
ctx.beginPath();
ctx.moveTo(x, y);
} else {
ctx.strokeStyle = "#F00";
ctx.lineTo(x, y);
}
angle += segmentAngleInc;
}
ctx.closePath();
ctx.stroke();
renderText(angleOffset);
renderButtons();
}
function renderText(angle) {
//# testo sgart.it
ctx.fillStyle = "#800";
ctx.font = "20px Arial";
ctx.textAlign = "right";
ctx.textBaseline = "top";
ctx.fillText("SGART.IT", canvas.width - 20, 20);
// visualizzo l'angolo corrente
ctx.fillStyle = "#080";
ctx.font = "20px Arial";
ctx.textAlign = "left";
ctx.textBaseline = "top";
ctx.fillText("angolo: " + (angle * RAD_DEG * 10 | 0) / 10, 20, 20);
}
function renderButtons() {
ctx.strokeStyle = "#444";
ctx.fillStyle = "#444";
ctx.textAlign = "center";
// SEGMENT
ctx.strokeRect(btnSegmentMinus.x, btnSegmentMinus.y, btnSegmentMinus.w, btnSegmentMinus.h);
ctx.strokeRect(btnSegmentPlus.x, btnSegmentPlus.y, btnSegmentPlus.w, btnSegmentPlus.h);
// SPEED
ctx.strokeRect(btnSpeedMinus.x, btnSpeedMinus.y, btnSpeedMinus.w, btnSpeedMinus.h);
ctx.strokeRect(btnSpeedPlus.x, btnSpeedPlus.y, btnSpeedPlus.w, btnSpeedPlus.h);
ctx.textBaseline = "middle";
ctx.font = "30px Arial";
ctx.fillText(btnSegmentMinus.label, btnSegmentMinus.cx, btnSegmentMinus.cy);
ctx.fillText(btnSegmentPlus.label, btnSegmentPlus.cx, btnSegmentPlus.cy);
ctx.fillText(btnSpeedMinus.label, btnSpeedMinus.cx, btnSpeedMinus.cy);
ctx.fillText(btnSpeedPlus.label, btnSpeedPlus.cx, btnSpeedPlus.cy);
// visualizzo il numero di lati
ctx.fillStyle = "#080";
ctx.font = "20px Arial";
ctx.textAlign = "right";
ctx.textBaseline = "bottom";
ctx.fillText("lati: " + segment, canvas.width - 20, btnSegmentMinus.y - 10);
// visualizzo il numero di lati
ctx.textAlign = "left";
ctx.fillText("Velocità: " + (animationSpeedAngle * 100 | 0) / 10, 20, btnSegmentMinus.y - 10);
}
/* gestione ciclo di animazione */
let lastTime = new Date();
function loop() {
//calcolo il tempo passato tra un render e l'altro
const current = new Date();
const elapsed = current - lastTime; //circa 16 msec
updatePosition(elapsed);
render();
lastTime = current;
requestAnimationFrame(loop);
}
/* event */
function getCoordinates(event) {
//event.preventDefault();
//event.stopPropagation();
var coord = {
x: -1,
y: -1,
buttons: 0,
touch: false,
valid: false
};
if (event.type.substring(0, 5) == "touch") {
coord.touch = true;
if (event.targetTouches.length === 1) {
var ev = event.targetTouches[0];
var offset = ev.target.getBoundingClientRect();
var x = ev.clientX - offset.left;
var y = ev.clientY - offset.top;
coord.x = mouse.x = parseInt(x / zoom)
coord.y = mouse.y = parseInt(y / zoom);
mouse.radius = ev.radiusX;
coord.buttons = 1;
coord.valid = true;
} else if (event.type === "touchend") {
coord.x = mouse.x;
coord.y = mouse.y;
coord.valid = true;
}
} else {
coord.x = mouse.x = parseInt(event.offsetX / zoom);
coord.y = mouse.y = parseInt(event.offsetY / zoom);
coord.buttons = event.buttons;
coord.valid = true;
}
return coord;
}
function checkPointIsInRect(point, rect) {
return (point.x >= rect.x && point.x <= rect.x + rect.w
&& point.y >= rect.y && point.y <= rect.y + rect.h)
}
function handleClick(event) {
var coord = getCoordinates(event);
if (coord.valid === true) {
if (checkPointIsInRect(coord, btnSegmentPlus)) {
segment += SEGMENT_INC;
if (segment > SEGMENT_MAX) {
segment = SEGMENT_MAX;
}
} else if (checkPointIsInRect(coord, btnSegmentMinus)) {
segment -= SEGMENT_INC;
if (segment < SEGMENT_MIN) {
segment = SEGMENT_MIN;
}
} else if (checkPointIsInRect(coord, btnSpeedPlus)) {
if (animationSpeedAngle > 10) {
animationSpeedAngle += SPEED_INC_10;
} else {
animationSpeedAngle += SPEED_INC;
}
if (animationSpeedAngle > SPEED_MAX) {
animationSpeedAngle = SPEED_MAX;
}
} else if (checkPointIsInRect(coord, btnSpeedMinus)) {
if (animationSpeedAngle > 10) {
animationSpeedAngle -= SPEED_INC_10;
} else {
animationSpeedAngle -= SPEED_INC;
}
if (animationSpeedAngle < SPEED_MIN) {
animationSpeedAngle = SPEED_MIN;
}
}
}
}
function initButtons() {
var w = canvas.width;
var h = canvas.height;
var bw = 40;
var bh = bw;
// segment
btnSegmentMinus = { x: w - bw - 20, y: h - bh - 20, w: bw, h: bh, cx: 0, cy: 0, label: "-" };
btnSegmentMinus.cx = btnSegmentMinus.x + btnSegmentMinus.w / 2;
btnSegmentMinus.cy = btnSegmentMinus.y + btnSegmentMinus.h / 2;
btnSegmentPlus = { x: w - bw * 2 - 20 - 5, y: h - bh - 20, w: bw, h: bh, cx: 0, cy: 0, label: "+" };
btnSegmentPlus.cx = btnSegmentPlus.x + btnSegmentPlus.w / 2;
btnSegmentPlus.cy = btnSegmentPlus.y + btnSegmentPlus.h / 2;
// speed
btnSpeedMinus = { x: 20 + 5 + bw, y: h - bh - 20, w: bw, h: bh, cx: 0, cy: 0, label: "-" };
btnSpeedMinus.cx = btnSpeedMinus.x + btnSpeedMinus.w / 2;
btnSpeedMinus.cy = btnSpeedMinus.y + btnSpeedMinus.h / 2;
btnSpeedPlus = { x: 20, y: h - bh - 20, w: bw, h: bh, cx: 0, cy: 0, label: "+" };
btnSpeedPlus.cx = btnSpeedPlus.x + btnSpeedPlus.w / 2;
btnSpeedPlus.cy = btnSpeedPlus.y + btnSpeedPlus.h / 2;
}
function init() {
wrapper = document.getElementById(idTemplate);
wrapper.style.position = "relative";
canvas = document.createElement("canvas");
canvas.width = CANVAS_WIDTH;
canvas.height = CANVAS_HEIGHT;
canvas.style.touchAction = "manipulation";
canvas.style.display = "block";
canvas.style.boxSizing = "border-box";
canvas.style.margin = "0 auto";
canvas.style.touchAction = "none"; // su tablet previene l'errore sgart-space-invaders.js:1620 [Intervention] Unable to preventDefault inside passive event listener due to target being treated as passive
canvas.style.userSelect = "none";
canvas.style.outline = "none";
wrapper.innerHTML = "";
wrapper.appendChild(canvas);
ctx = canvas.getContext("2d");
ctx.imageSmoothingEnabled = false;
initButtons();
canvas.addEventListener("click", handleClick);
loop();
}
init();
})("sgart-polygon");